An introduction to phased array radar sum-difference beam technology

The purpose of phased array formation sum-difference beam is to improve the angle measurement accuracy of the array. Due to the existence of the 3dB bandwidth of the antenna beam, in order to improve the angle measurement accuracy, the technology of sum-difference beam is often introduced to improve this index. The three output channels of the 26G radar area array are the sum beam channel, the azimuth difference channel and the pitch difference channel. The sampling method is the half-array method, that is, the sum beam can be obtained by adding the direction patterns of the left and right array elements, and the difference can be obtained by subtracting them. The beam, using the ratio of the two receiving channel signals, can obtain higher angle measurement accuracy in azimuth, and also use the ratio of the elevation difference channel and the beam channel to obtain higher elevation angle measurement accuracy. Since the principles of the two are the same, the following discussions are based on the azimuth and angle directions.

Principles:

Phased array radar can perform phase compensation for each transmitting or receiving channel to obtain the maximum in-phase signal superposition of the target point, so there will be a phase shifter (also called weighting, which gives each output signal introduce phase weighting). As shown in Figure 1 below:

The sum beam channel is formed by adding weighted receiving branches. If you want to introduce a difference beam channel, you need to divide the array into two at the front end, and sum and subtract the two arrays respectively to obtain a sum beam channel and a difference beam channel. as shown in picture 2:

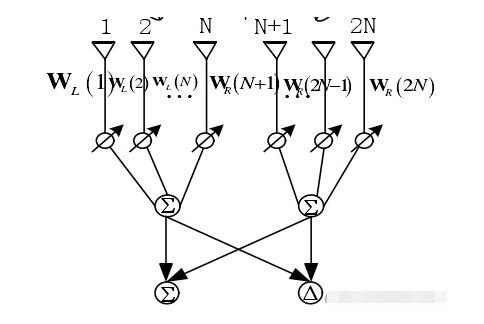
Now assume that there is a uniform equidistant linear array (direction angle) with an array element spacing of d, the number of array elements is 2N, and the actual direction of the target is a target of θ. Figure 2 above is an example diagram, and taking the first array element as a reference point, the steering vector of the left half array is

And the steering vector of the right half array is

Let W be the weighted value of the array. To make the beamforming point to θ0, WL= aL(θ0), WR= aR(θ0). Assume that the amplitude is ideal (the vibration element amplitude is the same, both are 1). Then the output of the left array:

For the sum beam then:

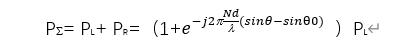
For the difference beam then:

The ratio of the two is:

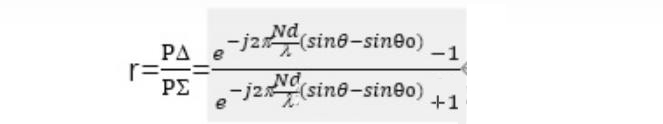
assume u=sinθ -sinθ 0， from Euler’s formula we know.

When the direction of the actual target θ=θ0, that is, when we set the phase shift to be exactly the actual orientation of the target, u=0, then the time difference beam channel is 0, and our angle measurement is accurate. And when the target deviates from the beam pointing very small, and u=sinθ-sinθ0 is very small, in the case of finitely large N and d,

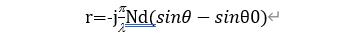
Further expand sinθ at θ0 by Taylor expansion,

Let Δθ=θ−θ0, then the relationship between the sum of the target deflection angle is:

It can be found from the above formula that the angle difference between the beam pointing and the actual target can be obtained by the difference between the beam sum and the ratio of the beam channel, so as to improve the accuracy of angle measurement. It is similar to the pitch difference, only the left and right fronts can be compared to the up and down fronts.